Descriptive Statistics

1 Sociology

1.1 Plots of the Sociology department

snet1_g <- igraph::graph_from_adjacency_matrix(snet1, mode = c("undirected"))
snet2_g <- igraph::graph_from_adjacency_matrix(snet2, mode = c("undirected"))
snet3_g <- igraph::graph_from_adjacency_matrix(snet3, mode = c("undirected"))

socdef_df$twitter_dum[socdef_df$id==36]<- 1
socdef_df$twitcol <- ifelse(socdef_df$twitter_dum == 0, "#56B4E9", "#66ff99")

#Dit zou ik nog even moeten checken of dit klopt, want er lijken ineens ties weg te vallen door die coördinaten toe te voegen?
l <- igraph::layout_with_mds(snet1_g)
l[14,1] <- 0
l1 <- igraph::layout_with_mds(snet2_g)
l1[14,1] <- 0
l2 <- igraph::layout_with_mds(snet3_g)
l2[14,1] <- 0

#Wat wil ik met de nummers in de plot, moet ik die nog veranderen in namen? Maar wil het graag anoniem houden.
plot(snet1_g, vertex.color = socdef_df$twitcol, vertex.size=socdef_df$ki,  vertex.size = 10, vertex.frame.color = "gray",
    vertex.label.color = "black", vertex.label.family = "Helvetica", vertex.label.cex = 0.7, vertex.label.dist = 0.8,
    edge.curved = 0.2, edge.arrow.size = 0.5, layout=l)

plot(snet2_g, vertex.color = socdef_df$twitcol, vertex.size=socdef_df$ki,  vertex.size = 10, vertex.frame.color = "gray",
    vertex.label.color = "black", vertex.label.family = "Helvetica", vertex.label.cex = 0.7, vertex.label.dist = 0.8,
    edge.curved = 0.2, edge.arrow.size = 0.5, layout=l1)

plot(snet3_g, vertex.color = socdef_df$twitcol, vertex.size=socdef_df$ki,  vertex.size = 10, vertex.frame.color = "gray",
    vertex.label.color = "black", vertex.label.family = "Helvetica", vertex.label.cex = 0.7, vertex.label.dist = 0.8,
    edge.curved = 0.2, edge.arrow.size = 0.5, layout=l2)

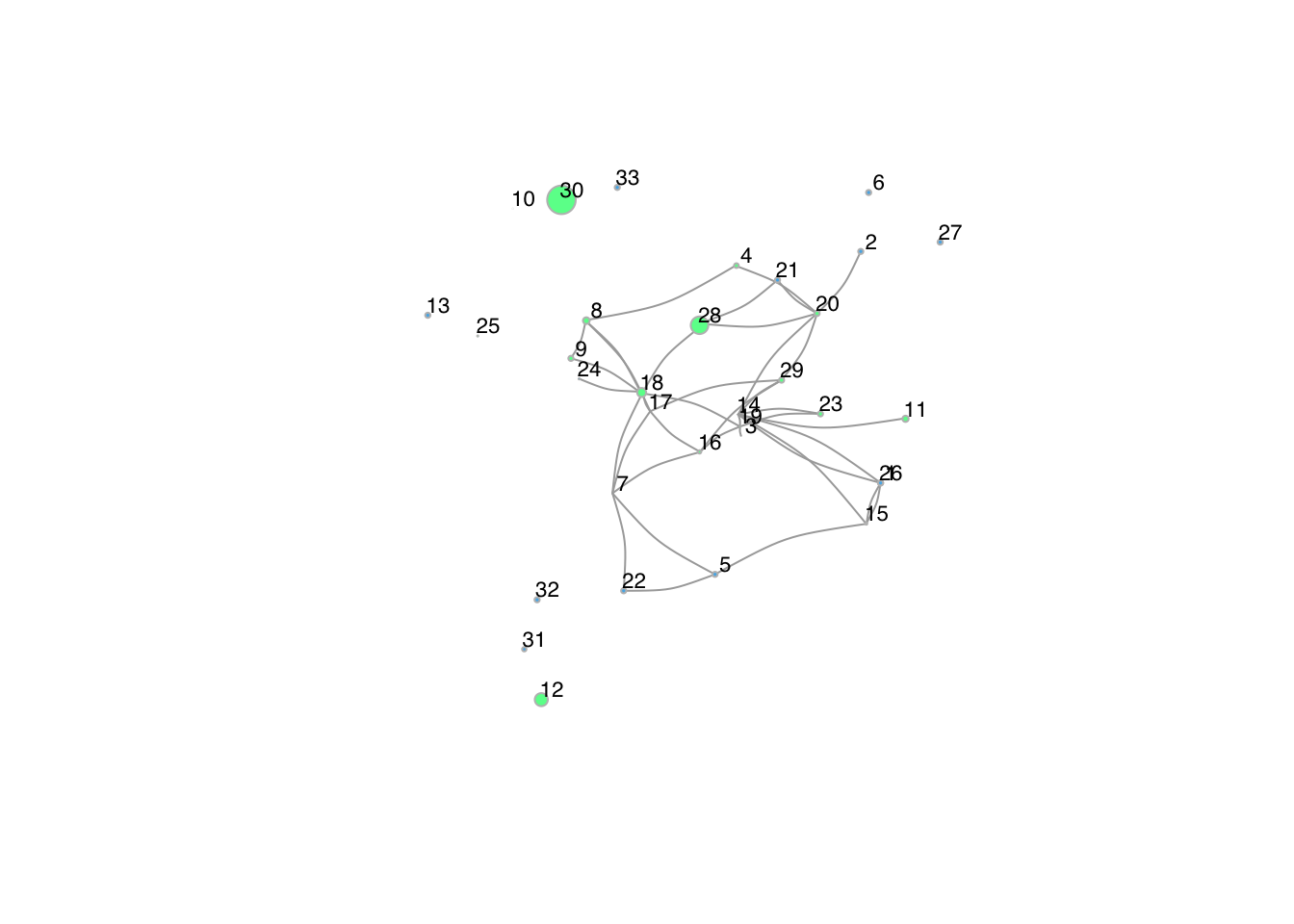
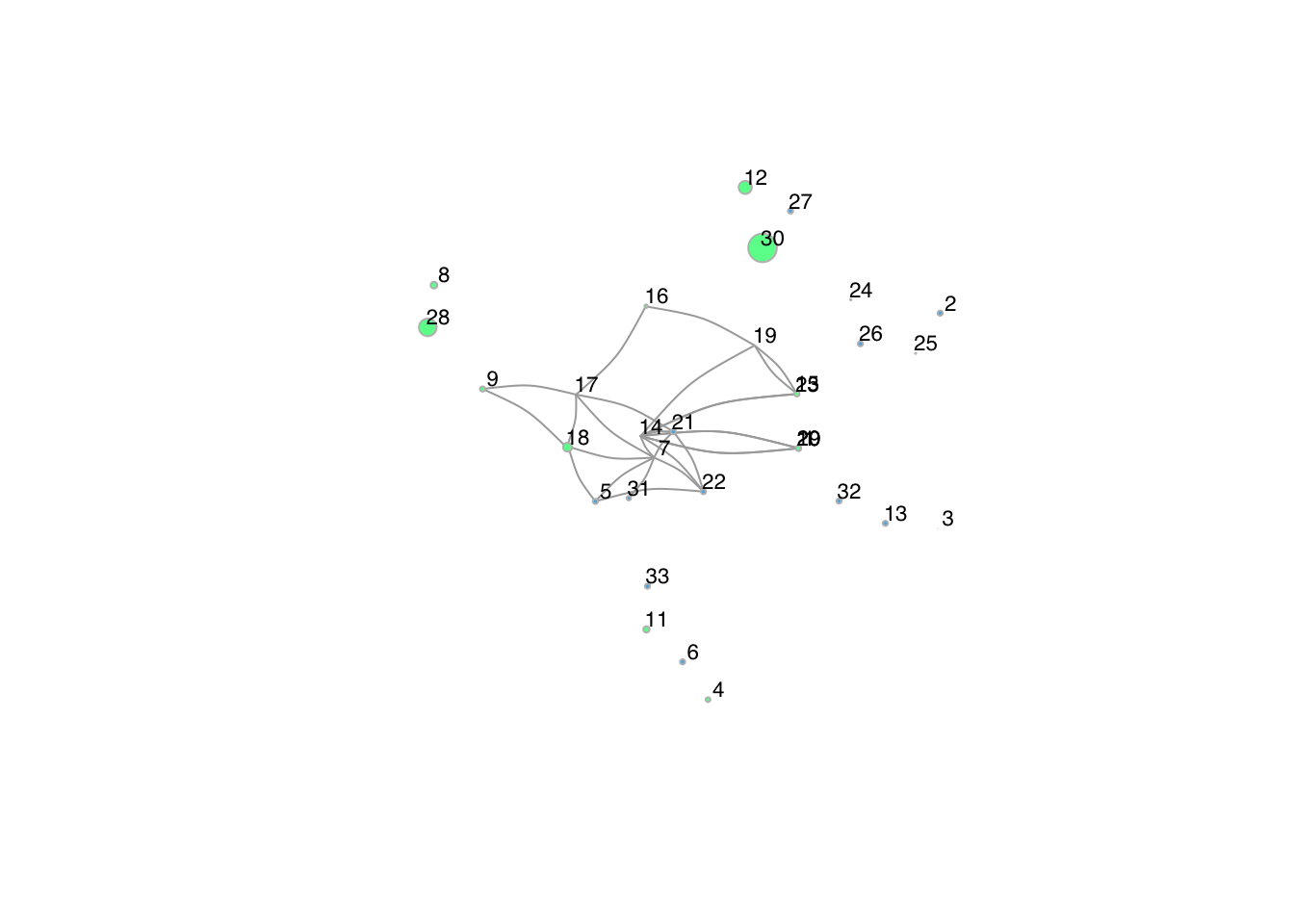
From the plots of the Sociology department it’s visible that there are quite a lot of co-publications within the network of Sociology. The first plot (of the year 2016-2017) shows that many scientists did not co-publish yet, but this increased over the years. This can be explained by the fact that a number of (younger) scientists did not yet work at the department in e.g. 2016, which results in no co-publication tie. Since node 14 is the most “productive” in the sense of co-publishing with others, I have put this node central in all the plots to show the evolution. This is an older scientist who has had more opportunities to publish with other individuals of the staff.

Another conclusion that can be drawn from the plot, is that individuals with a higher k-index do not have more co-publication ties. As I based the vertex size on the k-index, a higher k-index results in a larger vertex in the plot. It is visible that node 28 and 30 have the highest k-index, but this did not result in co-publications for node 30. For node 28, there is an increase of 3 co-publication ties when comparing the latter 2 plots. This could signal that this scientist is attractive to others because of the k-index, but this conclusion cannot be drawn yet from this plot alone. Therefore, this plot does not hint at selection effects based on k-index.

1.2 Descriptives of the Sociology network

sdegree <- igraph::degree(snet1_g)
sdegree2 <- igraph::degree(snet2_g)
sdegree3 <- igraph::degree(snet3_g)


#par(mfrow=c(3,1))
hist(sdegree, col="#99d6ff")

hist(sdegree2, col="#99d6ff")

hist(sdegree3, col="#99d6ff")

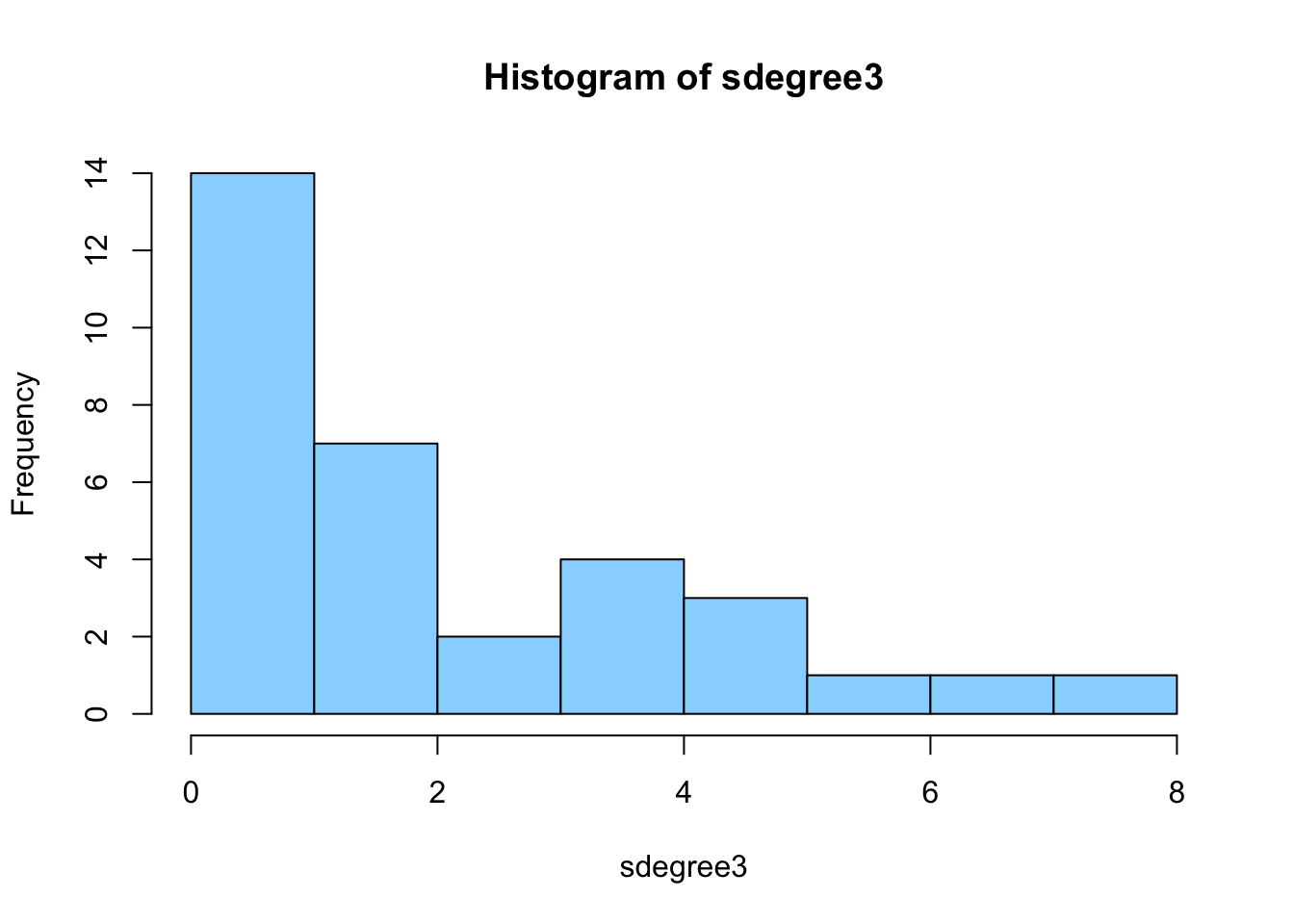
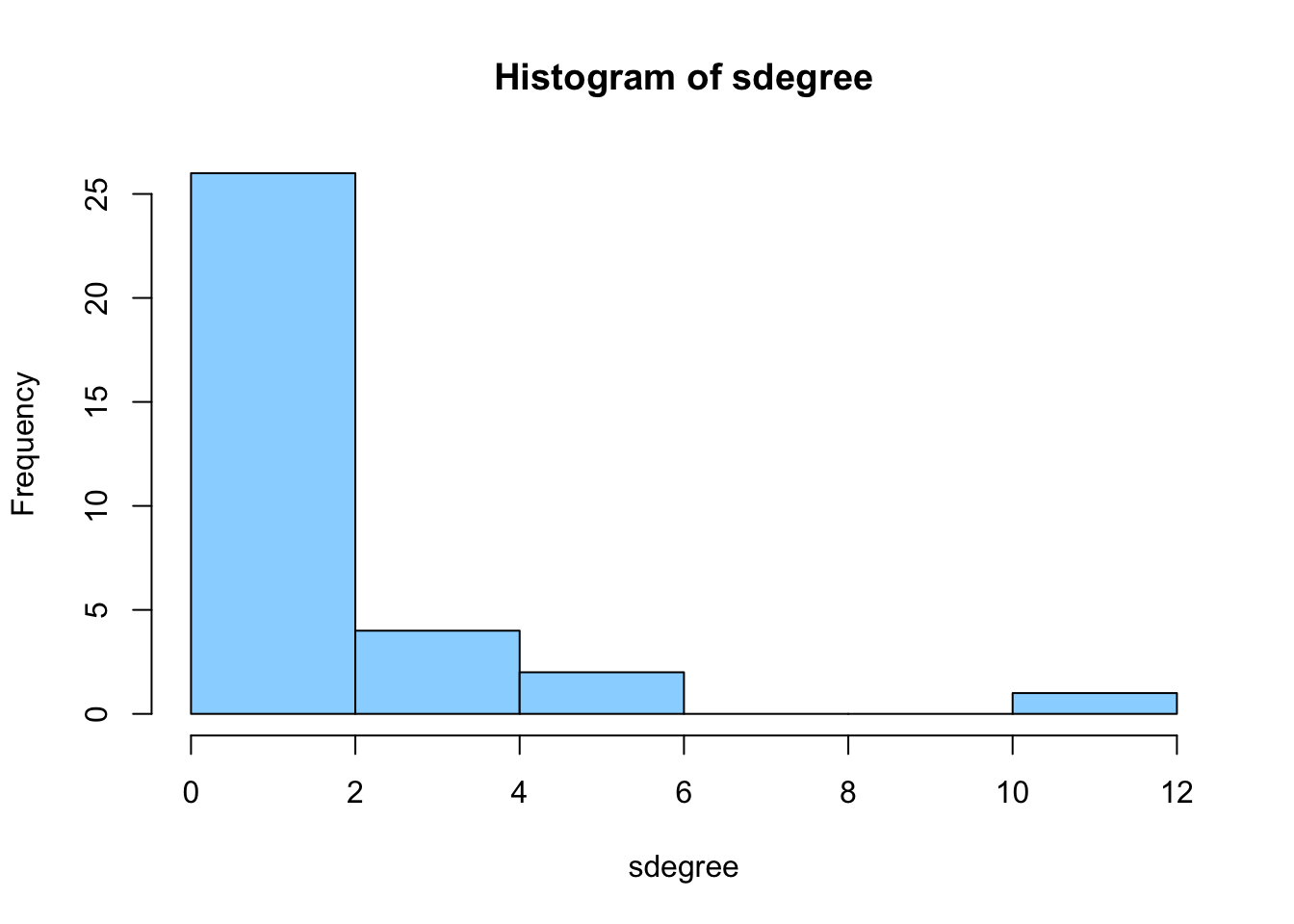
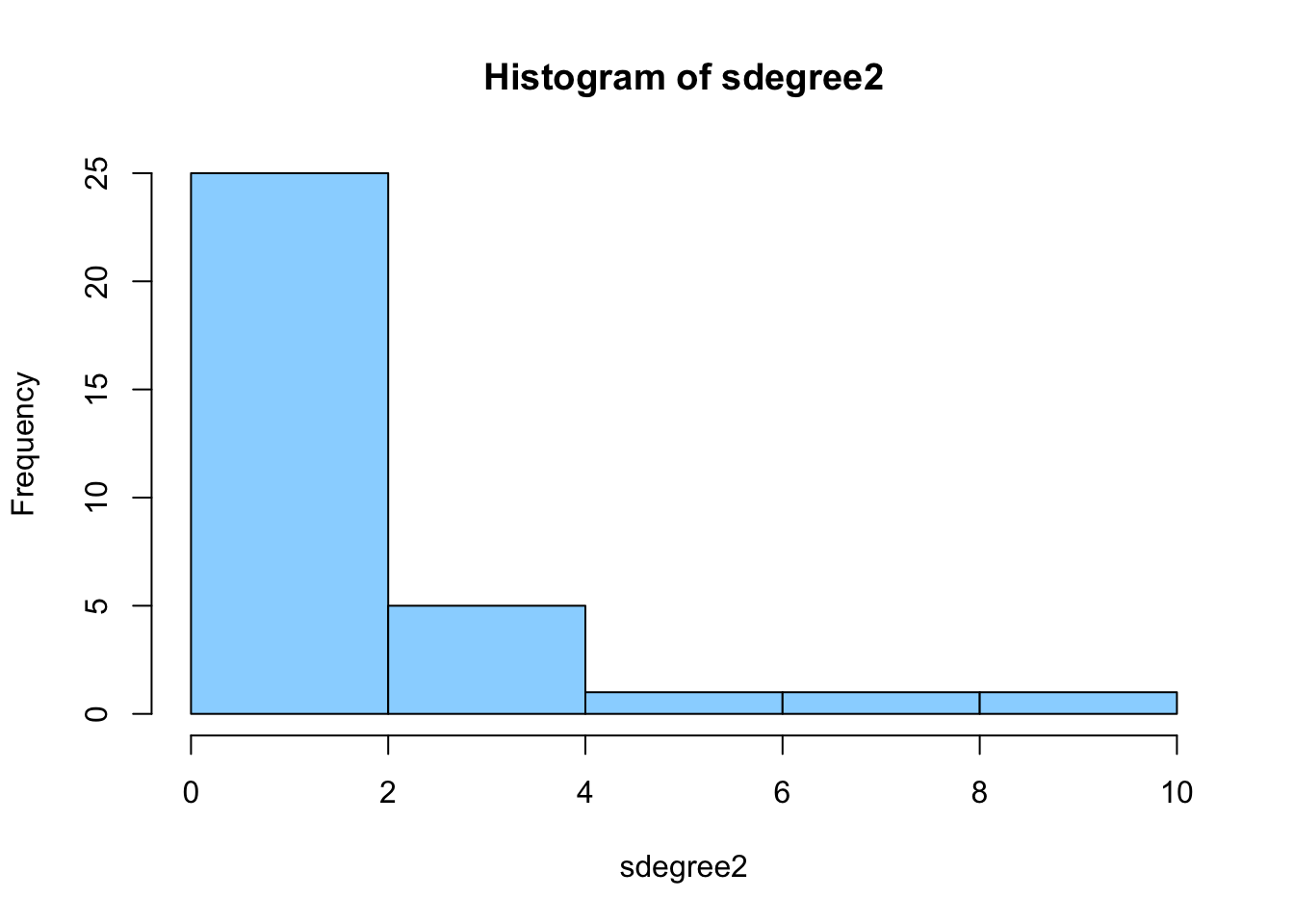
In the histograms above it is shown that the degree of the network is right-skewed. This means that most scientists in the network don’t have many other scientists within the department they co-published with. This is strongest for first the histogram, showing the first wave (2016-2017). In the following year, there still is a right-skewed distribution of the degrees, but there are a little more staff members in the tail of the distribution, meaning that these scientists have quite a lot of copublication ties. This occurs the most strongly in the histogram of the last years (2020 until now).

igraph::dyad.census(snet1_g)

#> $mut
#> [1] 26
#> 
#> $asym
#> [1] 0
#> 
#> $null
#> [1] 502

igraph::triad.census(snet1_g)

#>  [1] 4750    0  616    0    0    0    0    0    0    0   80    0    0    0    0   10

igraph::edge_density(snet1_g)

#> [1] 0.04924242

igraph::dyad.census(snet2_g)

#> $mut
#> [1] 27
#> 
#> $asym
#> [1] 0
#> 
#> $null
#> [1] 501

igraph::triad.census(snet2_g)

#>  [1] 4715    0  656    0    0    0    0    0    0    0   74    0    0    0    0   11

igraph::edge_density(snet2_g)

#> [1] 0.05113636

igraph::dyad.census(snet3_g)

#> $mut
#> [1] 38
#> 
#> $asym
#> [1] 0
#> 
#> $null
#> [1] 490

igraph::triad.census(snet3_g)

#>  [1] 4398    0  949    0    0    0    0    0    0    0   98    0    0    0    0   11

igraph::edge_density(snet3_g)

#> [1] 0.0719697

Regarding density and dyads in the network, there are 26 dyads in the first wave. The edge density is 0.049, which means that the number of edges existing in the network is relatively low compared to the the maximum number of edges there could possibly be. In the second wave, there is an increase of 1 dyad, and the edge density also has increased slightly towards a number of 0.051. In the last wave, there are 38 dyads and the edge density has increased to 0.072. Regarding the triad census [@davis1967structure], there are first 10 and then 11 complete triads, and first a decrease and then an increase of triads with one central node. Still, the triad 003 (with 3 null relations) occurs most. All in all, the co-publications within the network of sociology have increased, and over the years, the scientists at the department have used more of their opportunities to collaborate with members within the network.

igraph::transitivity(snet1_g)

#> [1] 0.2727273

igraph::transitivity(snet2_g)

#> [1] 0.3084112

igraph::transitivity(snet3_g)

#> [1] 0.2519084

Last but not least, the transitivity effect shows whether co-authors of co-authors become co-authors. For this network, no linear change can be observed. In the first wave, there is a transitivity number of 0.27. If one staff member A is connected to staff member B and staff member C, the probability is 0.27 that staff member B and C will also co-publish. In the second wave, we see that this probability has even increased to 0.308. In the last wave, the transitivity number is the lowest. Possibly, the fact that there are more mebers in the networks could increase the opportunities to co-publish with others, not depending on co-authors of co-authors.

1.3 K-index at the Sociology department

twsocbar <- ggplot2:::ggplot(socdef_df, aes(factor(twitter_dum), fill = factor(twitter_dum))) + geom_bar()
twsocbar <- twsocbar + scale_fill_manual(values=c("#56B4E9", "#66ff99"))
ggplotly(twsocbar)

Before diving into the k-index, it is insightful to see how many of the scientist at the department of Sociology have Twitter. In the above (interactive) graph, it is shown that 13 scientist do not have Twitter, while 20 scientists do have Twitter.

sel <- socdef_df$twitter_dum==1
hist(socdef_df$ki[sel], col="lightblue", border="darkblue")

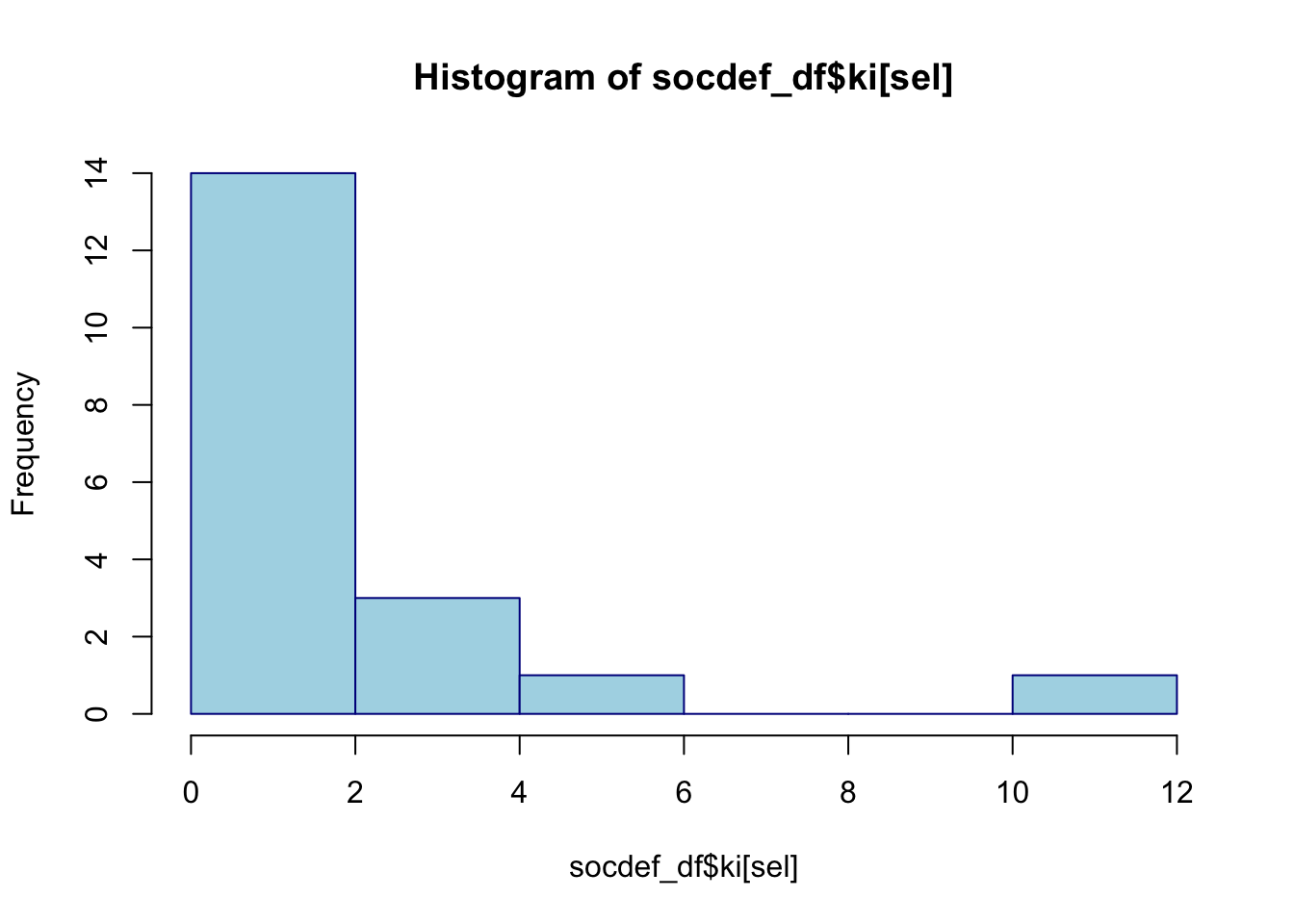
The above histogram shows the distribution of the k-index of scientists at the Sociology department. The distribution is right-skewed: Most scientists have a k-index between 0 and 2, and a few scientists have a high index. A few staff members have a k-index that would be categorized as “Kardashian Scientist” (Hall, 2014)

modelki <- lm(ki ~ gender + dutch + pub_first, data=socdef_df)
summary(modelki)

#> 
#> Call:
#> lm(formula = ki ~ gender + dutch + pub_first, data = socdef_df)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -3.5728 -0.9822 -0.0788  0.9981  4.8327 
#> 
#> Coefficients:
#>               Estimate Std. Error t value Pr(>|t|)   
#> (Intercept) -321.56977   95.80579  -3.356  0.00222 **
#> gendermale     2.08062    0.75754   2.747  0.01024 * 
#> dutch         -2.63707    0.92753  -2.843  0.00810 **
#> pub_first      0.16104    0.04749   3.391  0.00203 **
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 1.896 on 29 degrees of freedom
#> Multiple R-squared:  0.4394, Adjusted R-squared:  0.3814 
#> F-statistic: 7.577 on 3 and 29 DF,  p-value: 0.0006882

Lastly, it is insightful to see to what extent the k-index is predicted by other factors. The above linear regression teaches us that male scientist of Sociology have a significantly higher k-index than female staff members. It is also visible that Dutch scientists have a significantly lower k-index than non-Dutch scientists. Lastly, age is significantly related to the k-index: as age decreases, the k-index increases. Younger individuals thus have a higher k-index than older individuals. These effects can also be seen in the (interactive) graph below.

regplotsoc <- ggplot(socdef_df, mapping = aes(x = pub_first, y = ki, color=gender)) +
    geom_line() 
 
ggplotly(regplotsoc)

2 Data science

dnet1 <- dnet_array[ ,, 1]
dnet2 <- dnet_array[ ,, 2]
dnet3 <- dnet_array[ ,, 3]

diag(dnet1) <- 0
diag(dnet2) <- 0
diag(dnet3) <- 0

2.1 Plots of the Data Science department

dnet1_g <- igraph::graph_from_adjacency_matrix(dnet1, mode = c("undirected"))
dnet2_g <- igraph::graph_from_adjacency_matrix(dnet2, mode = c("undirected"))
dnet3_g <- igraph::graph_from_adjacency_matrix(dnet3, mode = c("undirected"))

datadef_df$twitcol <- ifelse(datadef_df$twitter_dum == 0, "#56B4E9", "#66ff99")

#Dit zou ik nog even moeten checken of dit klopt, want er lijken ineens ties weg te vallen door die coördinaten toe te voegen?
# l <- igraph::layout_with_mds(snet1_g)
# l[14,1] <- 0
# l1 <- igraph::layout_with_mds(snet2_g)
# l1[14,1] <- 0
# l2 <- igraph::layout_with_mds(snet3_g)
# l2[14,1] <- 0

#Wat wil ik met de nummers in de plot, moet ik die nog veranderen in namen? Maar wil het graag anoniem houden.
plot(dnet1_g, vertex.color = datadef_df$twitcol, vertex.size=datadef_df$ki,  vertex.size = 10, vertex.frame.color = "gray",
    vertex.label.color = "black", vertex.label.family = "Helvetica", vertex.label.cex = 0.7, vertex.label.dist = 0.8,
    edge.curved = 0.2, edge.arrow.size = 0.5)

plot(dnet2_g, vertex.color = datadef_df$twitcol, vertex.size=datadef_df$ki,  vertex.size = 10, vertex.frame.color = "gray",
    vertex.label.color = "black", vertex.label.family = "Helvetica", vertex.label.cex = 0.7, vertex.label.dist = 0.8,
    edge.curved = 0.2, edge.arrow.size = 0.5)

plot(dnet3_g, vertex.color = datadef_df$twitcol, vertex.size=datadef_df$ki,  vertex.size = 10, vertex.frame.color = "gray",
    vertex.label.color = "black", vertex.label.family = "Helvetica", vertex.label.cex = 0.7, vertex.label.dist = 0.8,
    edge.curved = 0.2, edge.arrow.size = 0.5)

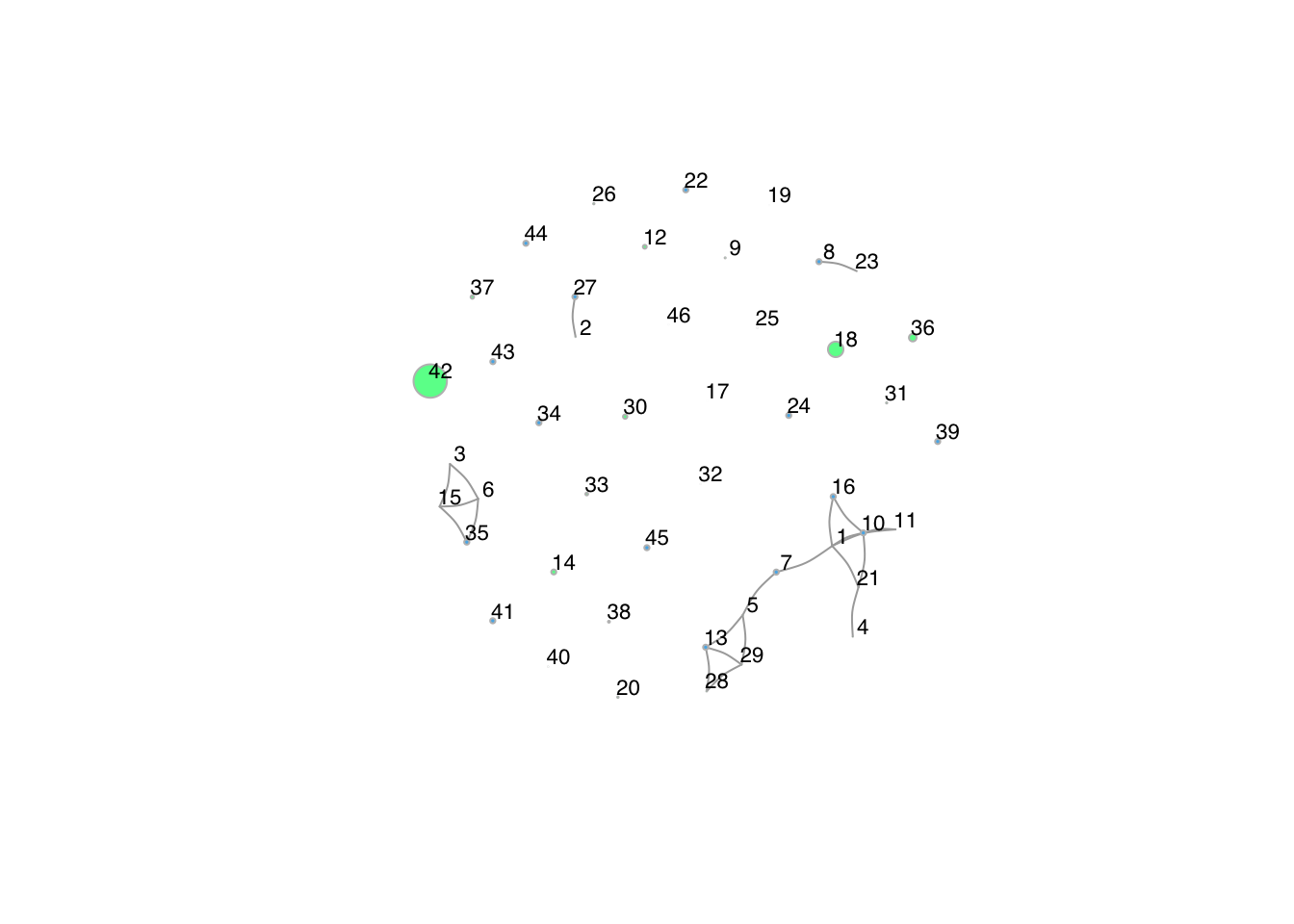
In the network plots of Data Science, it shows that during the year 2016-2017 there were not many co-publications. Just like at the Sociology department, it is likely that a high number of scientists did not work at the department yet. In the years 2018-2019, there is a strong increase in the co-publications of the staff members of Data Science. 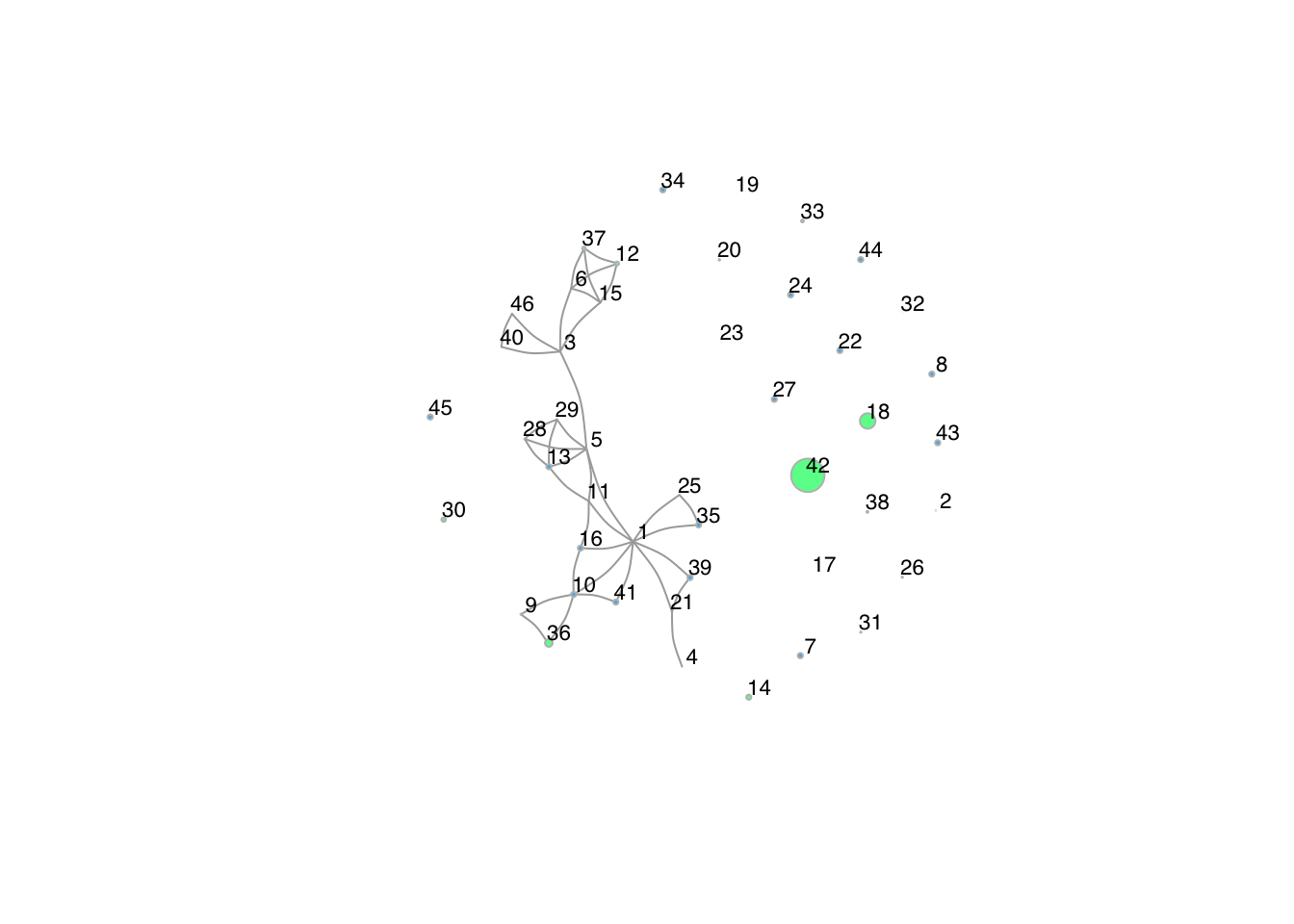Node 1, 3 and 5 seem to have a central role in the network, with the highest number of edges, and thus the most co-pulications with other scientists within the department. In the last plot, again an increase in co-publications is visible. Node 1, 3 and 5 still have a central role in the network, but there now are other nodes with a relative high number of co-publications as well.Similarly to the Sociology department, there are only a few nodes with a high k-index (shown by the largest vertex size), and it does not seem as if these scientists are especially attractive to others to co-publish an article.

2.2 Descriptives of the Data Science network

ddegree1 <- igraph::degree(dnet1_g)
hist(ddegree1, col="purple")

ddegree2 <- igraph::degree(dnet2_g)
hist(ddegree2, col="purple")

ddegree3 <- igraph::degree(dnet3_g)
hist(ddegree3, col="purple")

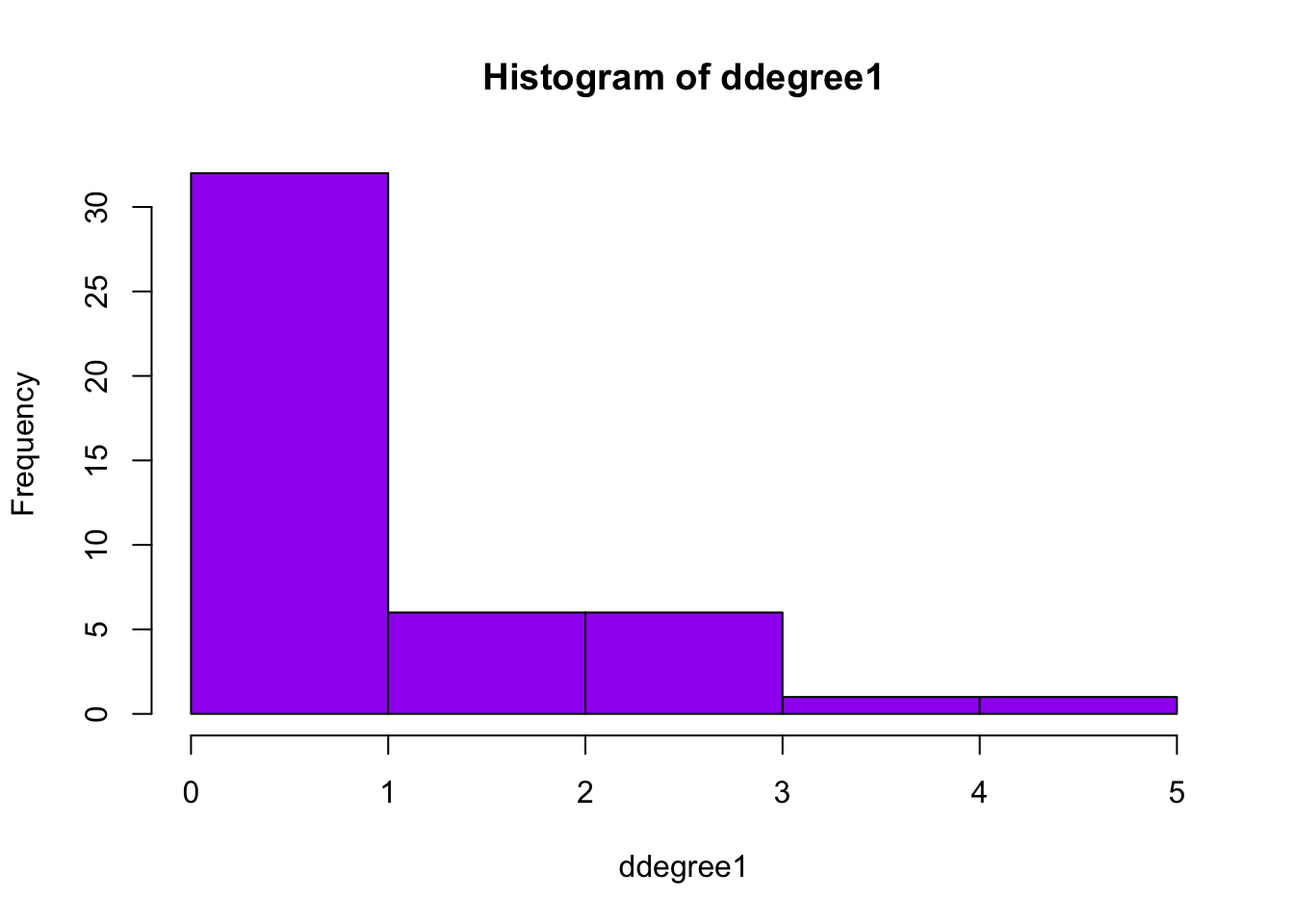
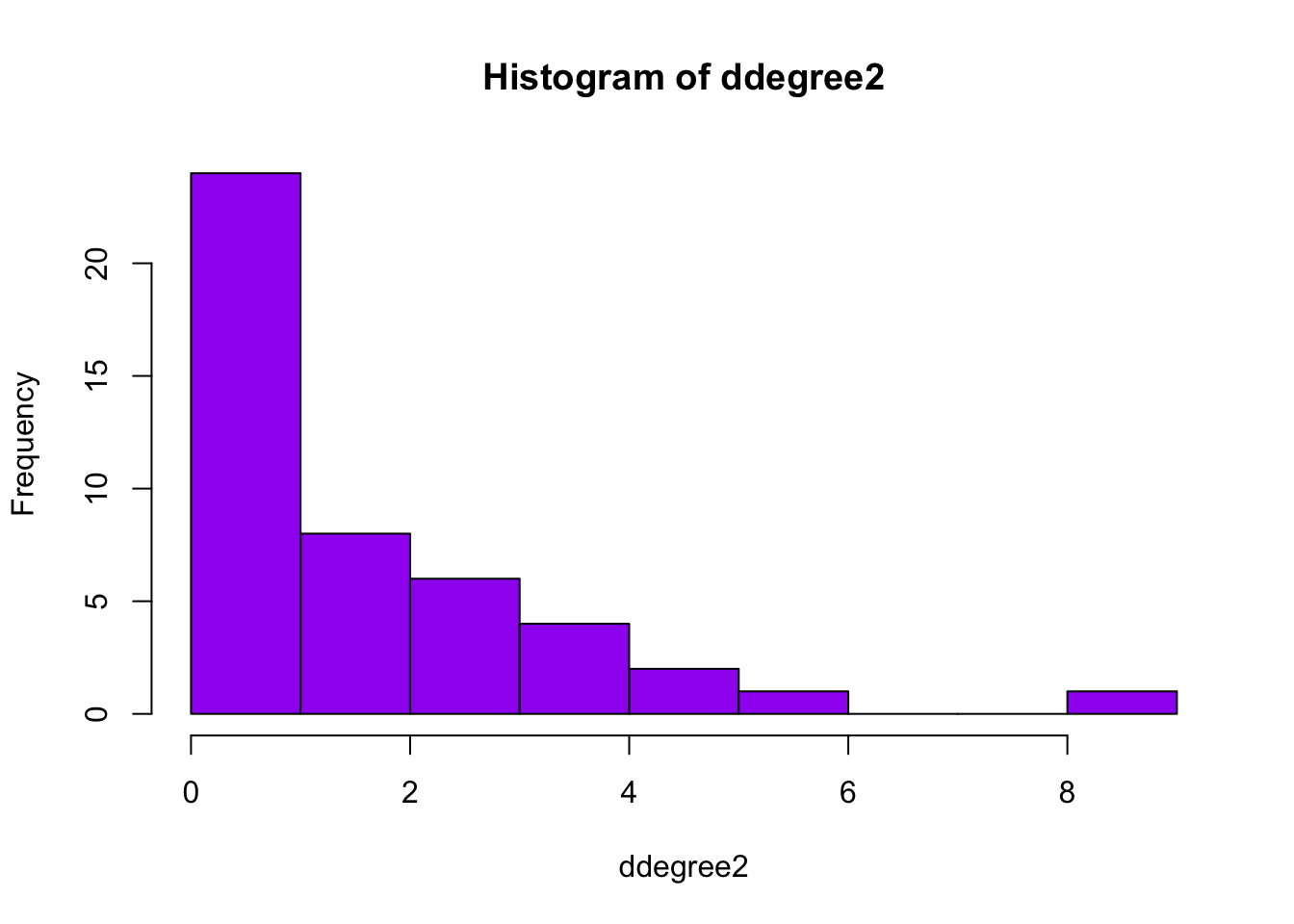
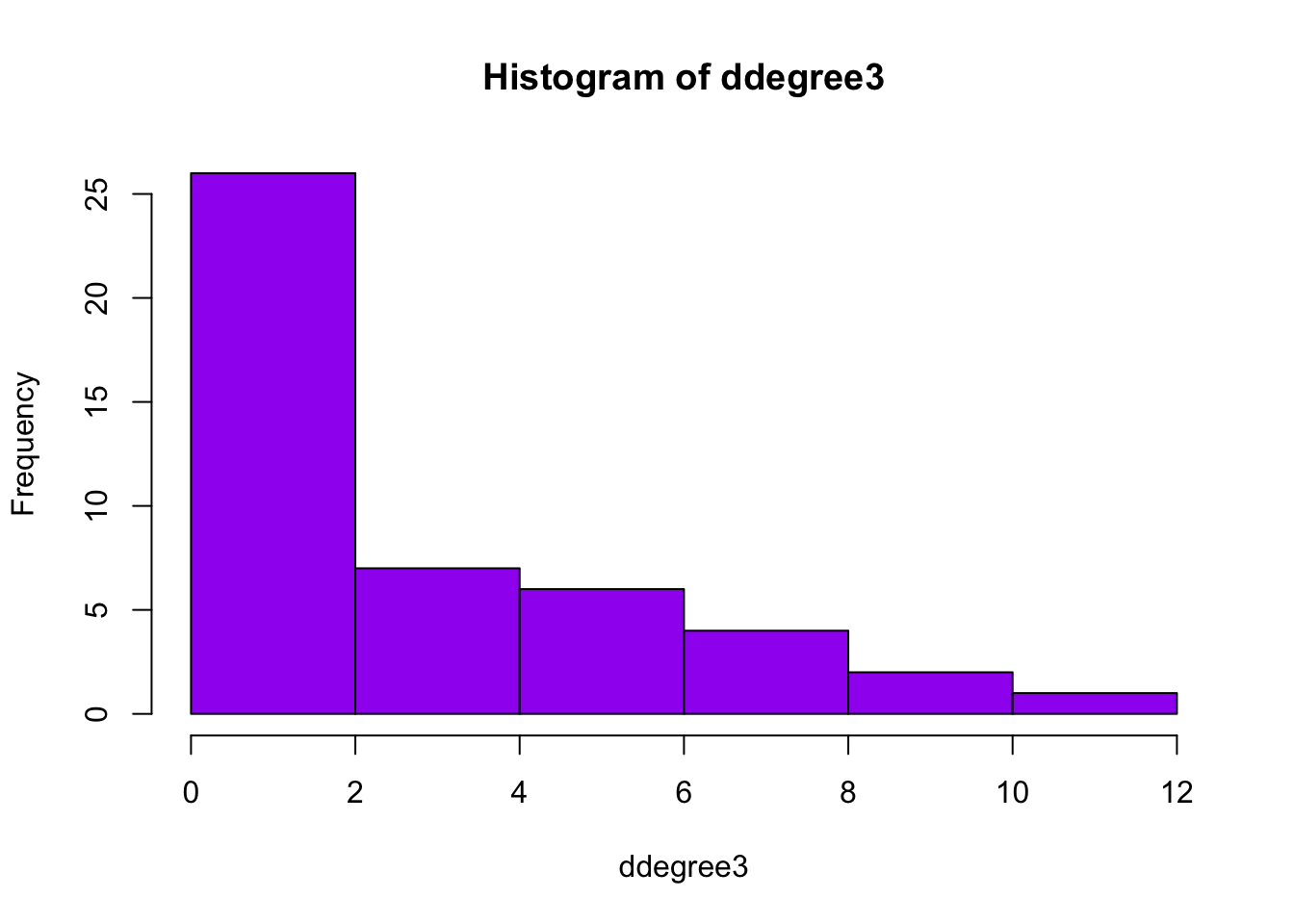Similarly to Sociology, the Data Science department shows a right-skewed distribution of the degrees. In the first wave, most scientists had not co-published, or only little. In the histogram of the second wave, it can be observed that the degrees remain skewed to the right. Furthermore, it is visible that one scientist has more than 8 copublications, and that in general, the number of outdegrees increased. However, most individuals still have no co-publications. In the last histogram, more scientists are in the tail, as also observed at the Sociology department. Furthermore, there are even staff scientist with 10-11 copublications. This is a higher number of copublications than observed at the Sociology department.

igraph::dyad.census(dnet1_g)

#> $mut
#> [1] 22
#> 
#> $asym
#> [1] 0
#> 
#> $null
#> [1] 1013

igraph::triad.census(dnet1_g)

#>  [1] 14245     0   909     0     0     0     0     0     0     0    19     0     0     0     0     7

igraph::edge_density(dnet1_g)

#> [1] 0.02125604

igraph::dyad.census(dnet2_g)

#> $mut
#> [1] 38
#> 
#> $asym
#> [1] 0
#> 
#> $null
#> [1] 997

igraph::triad.census(dnet2_g)

#>  [1] 13611     0  1484     0     0     0     0     0     0     0    67     0     0     0     0    18

igraph::edge_density(dnet2_g)

#> [1] 0.03671498

igraph::dyad.census(dnet3_g)

#> $mut
#> [1] 70
#> 
#> $asym
#> [1] 0
#> 
#> $null
#> [1] 965

igraph::triad.census(dnet3_g)

#>  [1] 12395     0  2537     0     0     0     0     0     0     0   201     0     0     0     0    47

igraph::edge_density(dnet3_g)

#> [1] 0.06763285

Looking at the dyad census and density, the number of dyads in 2016-2017 counts 22. The edge density is 0.0212. Both of these numbers are lower than at the Sociology department. In 2018-2019, the number of dyads has increased to 38 and the edge density has increased to 0.037. This is still lower than the edge density within the sociology department in the same years. In the last years, there are 70 dyads and the edge density increased towards a number of 0.068. This remains a little lower than the edge density of the Sociology department at that time. With regard to the triads, we see a similar pattern as at the Sociology department. However, there are more complete triads at Data Science, and this number has increased rather strongly over the years.

igraph::transitivity(dnet1_g)

#> [1] 0.525

igraph::transitivity(dnet2_g)

#> [1] 0.446281

igraph::transitivity(dnet3_g)

#> [1] 0.4122807

Regarding the transitivity, this has decreased at Data Science over the years. In the first period, the probability that scientist B and C - both as co-authors of scientist A - would co-publish was 0.52. In the next year, this decreased to a 45% chance, while in the last year this chance is 41,2%. Still, this is a higher number than observed at the Sociology department. Also, there is a linear decrease at the department of Data Science, while at the Sociology department no linear trend could be observed. In conclusion, staff members at Data Science are more likely to co-publish with co-authors of their co-authors than at Sociology, which is in line with the larger increase in triads.

2.3 K-index at the department of Data Science

twdatbar <- ggplot2:::ggplot(datadef_df, aes(factor(twitter_dum), fill = factor(twitter_dum))) + geom_bar()
twdatbar <- twdatbar + scale_fill_manual(values=c("#56B4E9", "#66ff99"))
ggplotly(twdatbar)

At the Data Science department, the majority of scientist has a Twitter account: 30 scientists have a Twitter account while 16 do not have one.

sel2 <- datadef_df$twitter_dum==1
hist(datadef_df$ki[sel2], col="red")

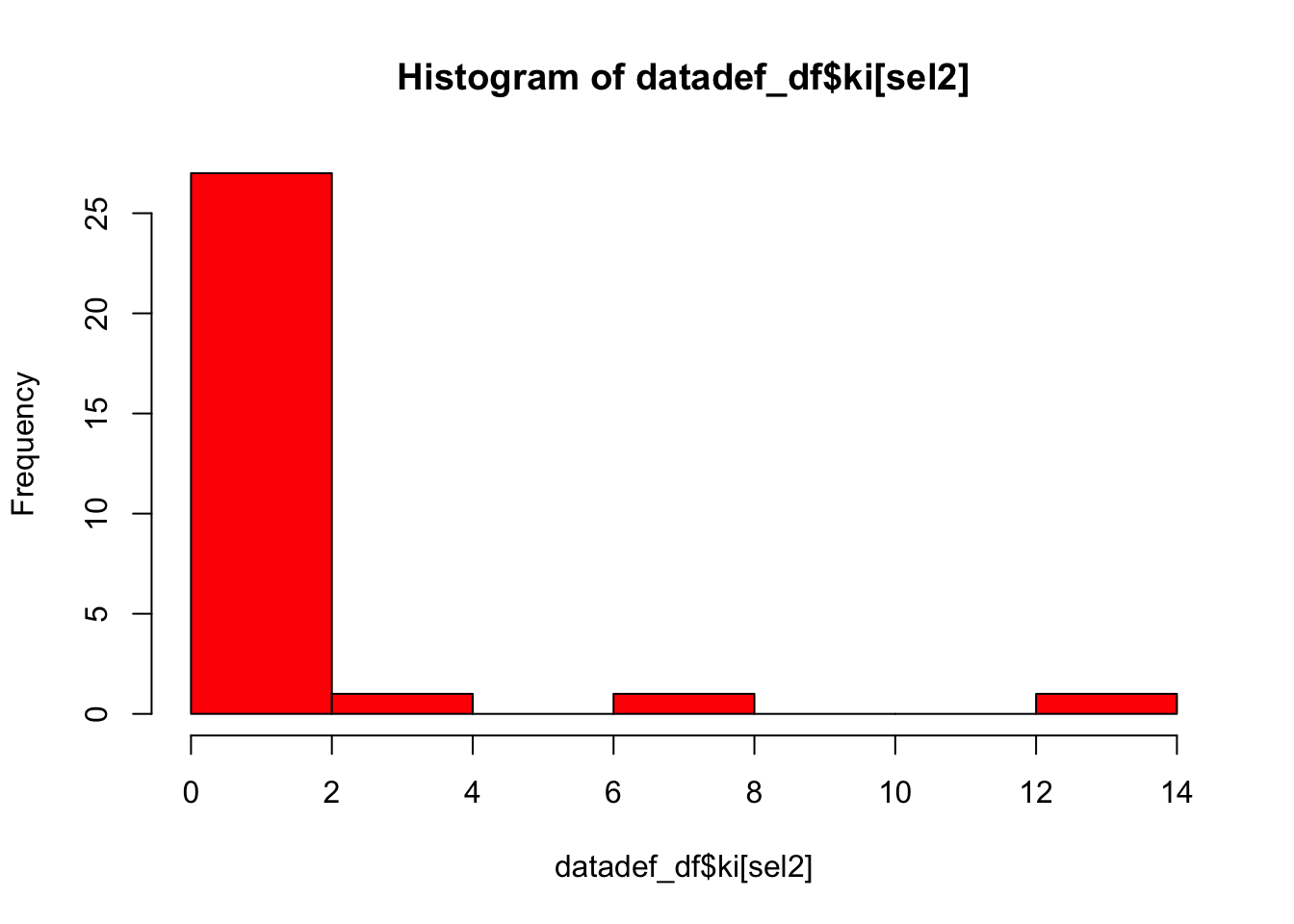The histogram shows that at the Data Science department, the distribution of the k-index is even more skewed than at the Sociology department. Most scientist have a k-index between 0 and 1, while only a few scientists have a k-index higher than that. Approximately two scientist would be categorized as “Kardashian Scientists” by Hall (2014)

modelki2 <- lm(ki ~ gender + dutch + pub_first, data=datadef_df)
summary(modelki2)

#> 
#> Call:
#> lm(formula = ki ~ gender + dutch + pub_first, data = datadef_df)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -1.5814 -0.9685 -0.4150  0.2484 11.7131 
#> 
#> Coefficients:
#>               Estimate Std. Error t value Pr(>|t|)  
#> (Intercept) -127.56740   61.00338  -2.091   0.0426 *
#> gendermale    -0.01333    0.70774  -0.019   0.9851  
#> dutch         -0.14260    0.72191  -0.198   0.8444  
#> pub_first      0.06392    0.03033   2.107   0.0411 *
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 2.116 on 42 degrees of freedom
#> Multiple R-squared:  0.09806,    Adjusted R-squared:  0.03364 
#> F-statistic: 1.522 on 3 and 42 DF,  p-value: 0.2227

At the Data Science department, the k-index is predicted differently than at the Sociology department when looking at the linear regression above. For the Data Science department, the effect of gender and ethnicity are not significant. Age is a significant predictor of the k-index. The younger the scientist, the higher the k-index. In the (interactive) plot below, it is also visible that gender and age are lesser determinants of the k-index than at the Sociology department.

# Dit nog bij assigning gender neerzetten (webscraping)
datadef_df$gender[datadef_df$id==261] <- "male"
datadef_df$gender[datadef_df$id==273] <- "male"

regplotdat <- ggplot(datadef_df, mapping = aes(x = pub_first, y = ki, color=gender)) +
    geom_line() 
 
ggplotly(regplotdat)

3 Comparison of the two departments

When comparing the two departments, there are some things worth noting. Regarding the network structure, the density of the co-publication network of Sociology is higher than that of the Data Science department. Within Sociology, scientists thus co-publish more with others of the same department, but at both cases the density is low. This shows that at both departments the co-publication network is rather sparse. This is not strange, as within academia it is not always possible to co-publish with any scientist in the network, as they might have different research interests. The transitivity differs as well between the two departments. The transitivity is higher at Data Science than at Sociology. This signals that it is more common among Data Scientists to publish articles with co-authors of co-authors.

With regard to Twitter and the k-index, the descriptives show that at both departments, the majority has a Twitter account. At the Data Science department, most scientists have a very low k-index with some exceptions, while at the Sociology department there are a few more scientists with a k-index above 1. This could show that for Sociologists, Twitter activity may be considered as more important than for Data Scientists, and for Sociologists the actual scientific output in terms of articles might be less important. Possibly, this could be explained by the fact that Sociologists would like to engage with society to share their research, as this society is often the research topic. However, for both departments, there are no clear hints that these scientists with a high k-index have more or less co-publications than scientists with a lower k-index.